Satz von König (Graphentheorie)
Der Satz von König ist ein grundlegender Satz aus dem mathematischen Gebiet der Graphentheorie, der für bipartite Graphen einen Zusammenhang zwischen einer größten Paarung und einer kleinsten Knotenüberdeckung aufzeigt. Er lautet:[1]
- In einem bipartiten Graphen ist die Größe einer größten Paarung gleich der Größe einer kleinsten Knotenüberdeckung.[A 1]
Der Satz ist nach dem ungarischen Mathematiker Dénes Kőnig benannt, der ihn 1931 bewiesen hat. Er ist, wie sich zeigen lässt, als gleichwertig mit dem Hall'schen Heiratssatz aufzufassen, weswegen er auch als Satz von König–Hall (englisch König–Hall theorem) bekannt ist.[2][3] Darüber hinaus hat der Mathematiker Jenő Egerváry – unabhängig von König und ebenfalls im Jahre 1931 – eine allgemeinere Fassung des Theorems für gewichtete Graphen bewiesen.[4][5] Deshalb wird der Satz manchmal auch als Satz von König–Egerváry (englisch König–Egerváry theorem) bezeichnet.
Der Satz lässt sich auch auf unendliche Graphen übertragen, wie schon Paul Erdős vermutete und wie Ron Aharoni bewies.[6][7]
Beispiel
[Bearbeiten | Quelltext bearbeiten]Ein Beispiel eines bipartiten Graphen, mit größter Paarung (blau) und kleinster Knotenüberdeckung (rot):
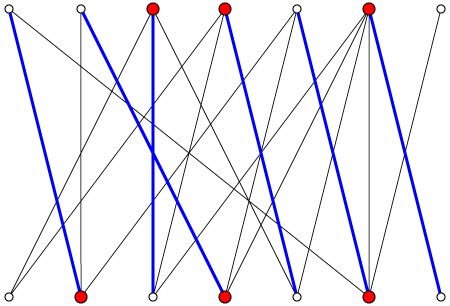
Algorithmus
[Bearbeiten | Quelltext bearbeiten]Dieser Algorithmus beschreibt wie man aus einer größten Paarung die kleinste Knotenüberdeckung erhält. Eine größte Paarung kann beispielsweise mit dem Algorithmus von Hopcroft und Karp berechnet werden. Die beiden Knotenmengen des bipartiten Graphen werden in Folge mit (oben) und (unten) bezeichnet.
- Eine größte Paarung berechnen.
- Alle nicht in der Paarung enthaltenen Knoten aus werden in eingefügt.
- Auf nicht in der Paarung enthaltenen Kanten gehen wir von diesen Knoten nach . Alle besuchten Knoten werden in eingefügt.
- Von den so erreichten Knoten in gehen wir auf in der Paarung enthaltenen Kanten wieder nach . Alle besuchten Knoten werden in eingefügt.
- Wiederhole die beiden vorherigen Schritte, solange bis keine neuen Knoten mehr in eingefügt werden.
- Die kleinste Knotenüberdeckung ergibt sich aus
Variante für gewichtete Graphen
[Bearbeiten | Quelltext bearbeiten]Bei der durch Jenő Egerváry (unabhängig von König) gegebenen Variante des Theorems für gewichtete Graphen betrachtet man bipartite Graphen mit einer Gewichtsfunktion , die jeder Kante im Graphen eine nichtnegative ganze Zahl zuordnet.[5] Eine gewichtete Knotenüberdeckung von ist eine Funktion die jedem Knoten im Graphen eine nichtnegative ganze Zahl zuordnet, sodass für alle Kanten gilt. Das Gewicht von is durch gegeben. Der Satz lautet dann wie folgt:
- In einem vollständigen bipartiten Graphen mit und einer Gewichtsfunktion , entspricht das maximale Gewicht einer Paarung dem minimalen Gewicht einer gewichteten Knotenüberdeckung von .
Version des Satzes mit binären Matrizen
[Bearbeiten | Quelltext bearbeiten]Berücksichtigt man – vor dem Hintergrund des Heiratssatzes – den Zusammenhang zwischen Adjazenzmatrizen und Graphen, so gewinnt man die folgende Version des Satzes:.[8][9][10][A 2]
- In einer binären Matrix ist die minimale Anzahl von Reihen, die benötigt werden, um alle Einsen der Matrix zu erfassen, gleich der maximalen Anzahl paarweise unabhängiger Einsen.
Verwandte Sätze
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Frank Harary: Graphentheorie. R. Oldenbourg Verlag, München, Wien 1974, ISBN 3-486-34191-X.
- Dieter Jungnickel: Transversaltheorie (= Mathematik und ihre Anwendungen in Physik und Technik. Band 39). Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig 1982 (MR0706076).
- Stasys Jukna: Extremal Combinatorics (= Texts in Theoretical Computer Science). 2. Auflage. Springer-Verlag, Heidelberg, Dordrecht, London, New York 2011, ISBN 978-3-642-17363-9 (MR2865719).
- Henryk Minc: Nonnegative Matrices (= Wiley-Interscience Series in Discrete Mathematics and Optimization). John Wiley & Sons, Inc., New York 1988, ISBN 0-471-83966-3 (MR0932967).
- Philip F. Reichmeider: The Equivalence of Some Combinatorial Matching Theorems. Polygonal Publishing House, Washington, NJ 1984, ISBN 0-936428-09-0 (MR0781348).
- Lutz Volkmann: Fundamente der Graphentheorie. Springer Verlag, Wien, New York 1996, ISBN 3-211-82774-9 (MR1392955).
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: König-Egeváry Theorem. In: MathWorld (englisch).
- Beweis zum Satz von König (PDF; 286 kB)
- Eintrag König theorem in der Encyclopedia of Mathematics (EoM)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Klaus Wagner: Graphentheorie. Bibliographisches Institut Hochschultaschenbücher, Mannheim 1970, ISBN 3-411-00248-4, Satz 9.9
- ↑ Lutz Volkmann: Fundamente der Graphentheorie. 1996, S. xviii, S. 119–123
- ↑ Philip F. Reichmeider: The Equivalence of Some Combinatorial Matching Theorems. 1984, S. 24–53
- ↑ Jenő Egerváry: Matrixok kombinatorius tulajdonságairól. In: Matematikai és Fizikai Lapok. Band 38, 1931, S. 16–28 (On combinatorial properties of matrices).
- ↑ a b Harold W. Kuhn: On combinatorial properties of matrices. In: George Washington University (Hrsg.): Logistics Papers. Band 11, 1955, S. 1–11.
- ↑ Aharoni, König's duality theorem for infinite bipartite graphs, Journal of the London Mathematical Society, Band 2, 1984, S. 1–12
- ↑ Aharoni, On a duality principle in infinite bipartite graphs, Journal of the London Mathematical Society, Band 2, 1983, S. 385–392
- ↑ Frank Harary: Graphentheorie. 1974, S. 63–64
- ↑ Stasys Jukna: Extremal Combinatorics. 2011, S. 81–83
- ↑ Philip F. Reichmeider: The Equivalence of Some Combinatorial Matching Theorems. 1984, S. 31–32
Anmerkungen
[Bearbeiten | Quelltext bearbeiten]- ↑ Hier versteht man unter Größe die Anzahl der Elemente der jeweiligen Menge.
- ↑ Die Zeilen und Spalten einer Matrix nennt man zusammengefasst Reihen (englisch lines). Weiter versteht man unter einer binären Matrix eine solche, deren Elemente alle gleich Null oder gleich Eins sind. Sind hier zwei Einsen in ein und derselben Reihe enthalten, so nennt man sie abhängig (englisch dependent) und andernfalls unabhängig (englisch independent).












